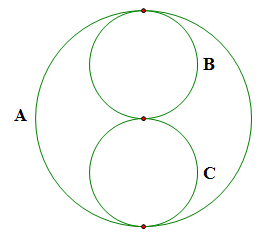
We begin with Sphere A with a radius of one. Inside that we put Sphere B and Sphere C, each with a radius of one half. They are placed so that they are internally tangent to Sphere A, and externally tangent to each other, as in the diagram. Now we would like to add some additional spheres to the interior of Sphere A.

1) What is the radius of the largest sphere that can be fit into the space inside Sphere A and outside Sphere B and Sphere C?
2) How many spheres of this size can be fit into that space?

Imagine that we add these spheres to the interior of Sphere A.

3) What is the radius of the largest sphere that can be fit into the remaining space?
4) How many of these spheres can be fit into that space?

Imagine that we again add these new spheres inside Sphere A, external to all of the other spheres.

5) Now, what is the radius of the largest sphere that can be fit into this smaller space?
6) And, how many of these spheres can be fit into that space?

Ok, that's enough. A rather surprising (to me, at least!) result of this process is that every sphere in this problem has a radius that is a rational number -- no radicals required. Another nice result is that the packing is very efficient -- it exhibits maximal tangency.